【基础知识精讲】
1.直线和平面的位置关系
一条直线和一个平面的位置关系有且只有如下三种关系:
(1)直线在平面内——直线上的所有点在平面内,根据公理1,如果直线上有两个点在平面内,那么这条直线上所有点都在这个平面内.
直线a在平面α内,记作a
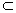 α.
α.(2)直线和平面相交——直线和平面有且只有一个公共点.
记作a∩α=A
(3)直线和平面平行——如果一条直线和一个平面没有公共点,那么这条直线和这个平面平行.记作a∥α.
直线和平面相交或平行两种情况统称直线在平面外,记作a
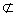 α.
α.2.直线和平面平行的判定
判定 如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.(简记“线线平行,则线面平行”)
即 a∥b,a
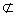 α,b
α,b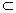 α
α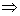 a∥α
a∥α证明 直线和平面平行的方法有:
①依定义采用反证法
②利用线面平行的判定定理
③面面平行的性质定理也可证明
3.直线和平面平行的性质定理
性质 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行(简记为“线面平行,线线平行”).
即 a∥α,a
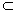 β,α∩β=b
β,α∩β=b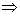 a∥b.
a∥b.这为证线线平行积累了方法:
①排除异面与相交 ②公理4 ③线面平行的性质定理
【重点难点解析】
本节重点是直线与平面的三种位置关系,直线和平面平行的判定和性质,难点是直线和平面平行的性质的应用.
例1 如图,ABCD和ABEF均为平行四边形,M为对角线AC上的一点,N为对角线FB上的一点,且有AM∶FN=AC∶BF,求证:MN∥平面CBE.
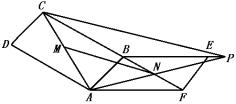
分析:欲证MN∥平面CBE,当然还是需要证明MN平行于平面CBE内的一条直线才行.题目上所给的是线段成比例的关系,因此本题必须通过三角形相似,由比例关系的变通,才能达到“线线平行”到“线面平行”的转化.
证:连AN并延长交BE的延长线于P.
∵ BE∥AF,∴ ΔBNP∽ΔFNA.
∴
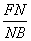 =
=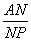 ,则
,则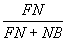 =
=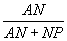 .
.即
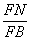 =
=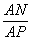 .
.又
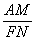 =
=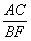 ,
,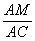 =
=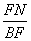 ,
,∴
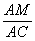 =
=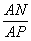 .
.∴ MN∥CP,CP
 平面CBE.
平面CBE.∴ MN∥平面CBE.
例2 一直线分别平行于两个相交平面,则这条直线与它们的交线平行.
已知:α∩β=a,l∥α,l∥β.求证:l∥a.
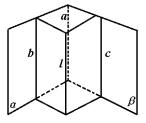
分析:由线面平行推出线线平行,再由线线平行推出线面平行,反复应用线面平行的判定和性质.
证明:过l作平面交α于b.∵l∥α,由性质定理知l∥b.
过l作平面交β于c.∵l∥β,由性质定理知l∥c.
∴ b∥c,显然c
 β.∴ b∥β.
β.∴ b∥β. 又 b
 α,α∩β=a,∴ b∥a.
α,α∩β=a,∴ b∥a. 又 l∥b.
∴ l∥a.
评注:本题在证明过程中注意文字语言、符号语言,图形语言的转换和使用.
例3 如图,在正四棱锥S—ABCD中,P在SC上,Q在SB上,R在SD上,且SP∶PC=1∶2,SQ∶SB=2∶3,SR∶RD=2∶1.求证:SA∥平面PQR.
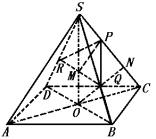
分析:根据直线和平面平行的判定定理,必须在平面PQR内找一条直线与AS平行即可.
证:连AC、BD,设交于O,连SO,连RQ交SO于M,取SC中点N,连ON,那么ON∥SA.
∵
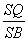 =
=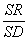 =
=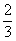
∴RQ∥BD
∴
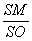 =
=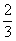 而
而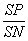 =
=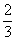
∴
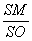 =
=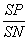 ∴PM∥ON
∴PM∥ON∵SA∥ON.∴SA∥PM,PM
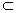 平面PQR
平面PQR∴ SA∥平面PQR.
评析:利用平几中的平行线截比例线段定理.
三角形的中位线性质等知识促成“线线平行”向“线面平行”的转化.
例4 证明:过平面上一点而与这平面的一条平行线平行的直线,在这平面上.
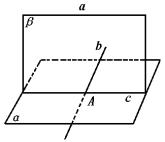
证明 如图,设直线a∥平面α,点A∈α,A∈直线b,b∥a,欲证b
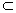 α.事实上,∵b∥a,可确定平面β,β与α有公共点A,∴α,B交于过A的直线c,∵a∥α,∴a∥c,从而在β上有三条直线,其中b、c均过点A且都与a平行.于是b、c重合,即b
α.事实上,∵b∥a,可确定平面β,β与α有公共点A,∴α,B交于过A的直线c,∵a∥α,∴a∥c,从而在β上有三条直线,其中b、c均过点A且都与a平行.于是b、c重合,即b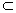 α.
α.【难题巧解点拨】
例1 S是空间四边形ABCD的对角线BD上任意一点,E、F分别在AD、CD上,且AE∶AD=CF∶CD,BE与AS相交于R,BF与SC相交于Q.求证:EF∥RQ.
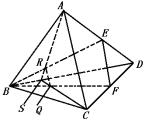
证 在ΔADC中,因AE∶AD=CF∶CD,故EF∥AC,而AC
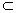 平面ACS,故EF∥平面ACS.而RQ=平面ACS∩平面RQEF,故EF∥RQ(线面平行性质定理).
平面ACS,故EF∥平面ACS.而RQ=平面ACS∩平面RQEF,故EF∥RQ(线面平行性质定理).例2 已知正方体ABCD—A′B′C′D′中,面对角线AB′、BC′上分别有两点E、F且B′E=C′F求证:EF∥平面AC.
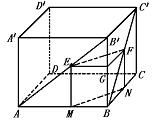
分析 如图,欲证EF∥平面AC,可证与平面AC内的一条直线平行,也可以证明EF所在平面与平面AC平行.
证法1 过E、F分别做AB、BC的垂线EM、FN交AB、BC于M、N,连接MN
∵BB′⊥平面AC ∴ BB′⊥AB,BB′⊥BC
∴EM⊥AB,FN⊥BC
∴EM∥FN,∵AB′=BC′,B′E=C′F
∴AE=BF又∠B′AB=∠C′BC=45°
∴RtΔAME≌RtΔBNF
∴EM=FN
∴四边形MNFE是平行四边形
∴EF∥MN又MN
 平面AC
平面AC∴EF∥平面AC
证法2 过E作EG∥AB交BB′于G,连GF
∴
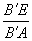 =
=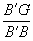
∵B′E=C′F,B′A=C′B
∴
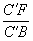 =
=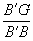 ∴FG∥B′C′∥BC
∴FG∥B′C′∥BC又∵EG∩FG=G,AB∩BC=B
∴平面EFG∥平面AC
又EF
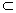 平面EFG
平面EFG∴EF∥平面AC
例3 如图,四边形EFGH为四面体A—BCD的一个截面,若截面为平行四边形,求证:(1)AB∥平面EFGH;(2)CD∥平面EFGH
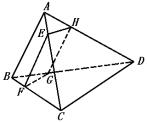
证明:(1)∵EFGH为平行四边形,∴EF∥HG,
∵HG
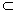 平面ABD,∴EF∥平面ABD.
平面ABD,∴EF∥平面ABD.∵EF
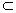 平面ABC,平面ABD∩平面ABC=AB.
平面ABC,平面ABD∩平面ABC=AB.∴EF∥AB,∴AB∥平面EFGH.
(2)同理可证:CD∥EH,∴CD∥平面EFGH.
评析:由线线平行
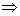 线面平行
线面平行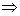 线线平行.
线线平行.【课本难题解答】
1.求证:如果两条平行线中的一条和一个平面相交,那么另一条也和这个平面相交.
已知:a∥b,a∩α=A,求证:b和α相交.
证明:假设b
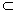 α或b∥α.
α或b∥α.若b
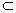 α,∵b∥a,∴a∥α.
α,∵b∥a,∴a∥α.这与a∩α=A矛盾,∴b
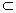 α不成立.
α不成立.若b∥α,设过a、b的平面与α交于c.
∵b∥α,∴b∥c,又a∥b ∴a∥c
∴a∥α这与a∩α=A矛盾.∴b∥α不成立.
∴b与α相交.
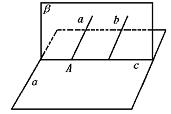
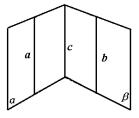
2.求证:如果两个相交平面分别经过两条平行直线中的一条,那么它们的交线和这条直线平行.
已知:a∥b,a
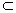 α,b
α,b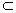 β,α∩β=c.
β,α∩β=c.求证:c∥a∥b
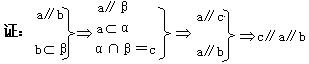
【命题趋势分析】
本节主要掌握直线和平面的位置关系的判定,直线与平面平行的证明与应用,它是高考中常考的内容,难度适中,因此学习好本节内容至关重要.
【典型热点考题】
例1 在下列命题中,真命题是( )
A.若直线m、n都平行平面α,则m∥n;
B.设α—l—β是直二面角,若直线m⊥l,则m⊥n,m⊥β;
C.若直线m、n在平面α内的射影是一个点和一条直线,且m⊥n,则n在α内或n与α平行;
D.设m、n是异面直线,若m和平面α平行,则n与α相交.
解 对于直线的平行有传递性,而两直线与平面的平行没有传递性故A不正确;平面与平面垂直可得出线面垂直,要一直线在一平面内且垂直于交线,而B中m不一定在α内,故不正确;对D来说存在平面同时和两异面直线平行,故不正确;应选C.
例2 设a、b是两条异面直线,在下列命题中正确的是( )
A.有且仅有一条直线与a、b都垂直
B.有一平面与a、b都垂直
C.过直线a有且仅有一平面与b平行
D.过空间中任一点必可作一条直线与a、b都相交
解 因为与异面直线a、b的公垂线平行的直线有无数条,所以A不对;若有平面与a、b都垂直,则a∥b不可能,所以B不对.若空间的一点与直线a(或b)确定的平面与另一条直线b(或a)平行,则过点与a相交的直线必在这个平面内,它不可能再与另一条直线相交,所以D不对,故选C.
例3 三个平面两两相交得三条交线,若有两条相交,则第三条必过交点;若有两条平行,则第三条必与之平行.
已知:α∩β=a,α∩
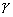 =b,
=b, 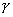 ∩α=c.
∩α=c.求证:要么a、b、c三线共点,要么a∥b∥c.
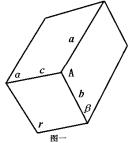
证明:①如图一,设a∩b=A,
∵α∩β=a.
∴a
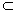 α而A∈a.
α而A∈a.∴A∈α.
又β∩
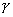 =b
=b∴b
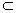
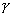 ,而A∈b.
,而A∈b.∴A∈
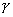 .
.则A∈α,A∈
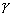 ,那么A在α、
,那么A在α、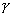 的交线c上.
的交线c上.从而a、b、c三线共点.
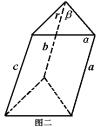
②如图二,若a∥b,显然c
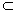
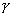 ,b
,b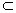
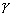
∴ a∥
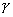
而 a
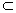 α, α∩
α, α∩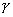 =c.
=c.∴ a∥c
从而 a∥b∥c
东莞耐斯机械近期倾力打造性价比最高的可以钻斜孔的六轴多功能深孔钻,并很快赢
得客户的认可。
六轴深孔钻床是一种以钻深孔为主,配有高精度数控转台B轴,滑台旋转轴A轴和铣削功能,
可一次装夹完成五面钻削加工和铣削加工,扩大了机床的加工范围,大大提高了加工精度
和工作效率,有效的节约了生产成本。
1.该机床集现代工业先进技术为一体:
2. 机械传动X、Y、Z、W、A轴采用高精度内循环滚珠丝杠。
3. X、Y、Z、W轴采用线性导轨,精度保持性好。
4. 机床配有深孔切削冷却系统,采用远距离控制系统,可根据钻孔的大小分别供应不同的流量和压力。
5. 机床主轴采用无级调速,调速范围广,功率配置合理
NCS6Z系列六轴多功能数控深孔钻铣床,集铣削、深孔加工于一体,让一次装夹实现多面多工序加工成为可能。
1、主轴(A轴)向上15度,向下25度高精度旋转。
2、主轴具有强力铣削功能(可安装刀盘)。
3、可配喷吸钻,实现高效率、高精度、高光洁度的大孔加工,光洁度可达0.4~0.8。
4、机床主体均为高强度铸件,具有高强度、高刚性,为机床的平稳运行提供有效保证。
使用行业:模具、机械制造行业,主要用于复杂零件的铣削,深孔加工。
东莞耐斯机械近期倾力打造功能最强大的NC系列合模机是耐斯公司针对中、大型模具,专推出的一款新型立式合模机。该种机型在传统立式合模机的基础上作了重大的技术改进。该系列合模机分磁盘式和压板式两种规格,模具可实现0-180°翻转。磁盘式采用电控永磁,无需上紧固螺丝,大大节约了锁模时间,采用PLC控制,人机界面操作简便、快捷、安全可靠。整机采用框架结构,机身焊后采用振动时效去应力处理,结构稳定,刚性好、变形小、寿命长,精度可长期保持。
耐斯NC立式合模机特点:
1. 机架采用焊接式分体结构,分体间用格林柱拉紧,经回火处理,刚度大、变形小。
2. 压板式上、下工作台及导轨均采用球墨铸铁制作,平面度好,精度高,变形量小。
3. 磁盘式采用电控永磁盘,断电不断磁,使用中无需供电,磁力强,既安全又省电。
4. 安全装置齐全,有安全光栅、防落油缸、锁紧油缸、安全支撑架等防护设备。
5. 液压系统采用吸震装置,减小液压冲击,保证设备精度。
6. 液压系统具有低压保护装置,防止碰穿、插穿位损坏。
7. 系统可采用高速合模产生冲击,使压印红丹效果极佳。
东莞耐斯机械翻模机平板翻模机特点:
液压平板翻模机跟机械式翻模机不同的是采用了液压系统作为动力驱动两块模板翻转带动模具翻身。设备的主要优点是平时不需要使用设备时可将两块模板放平成180度,更节约空间。
耐斯平板翻模机的主要特点:
1、机器可下沉安装,不占用生产空间。
2、采用进口电气配件,安全、可靠,操作方便。
2、两块模板分开翻转,平时不使用设备时在平放。
3、解决有些模具在传统90度翻模机上翻转后不方便装吊环的问题。
NCF系列翻模机技术参数:
| 型号 | NCF-5 | NCF-10 | NCF-15 | NCF-20 | NCF-30 | NCF-50 |
| 翻转能力(T) | 5 | 10 | 15 | 20 | 30 | 50 |
| 翻转时间(s) | 20 | 25 | 30 | 35 | 40 | 50 |
| 台面尺寸(mm) | 1100x1000 | 1400×1270 | 1600×1400 | 1800×1500 | 2000×1715 | 2200×2000 |
| 台面高度(mm) | 550 | 700 | 750 | 760 | 870 | 1000 |
| 外形尺寸(mm) | 1100x1500x1500 | 1400×1900×1980 | 1600×2200×2150 | 1800×2300×2260 | 2000×2500×2590 | 2200×2900×3000 |
| 中心尺寸(mm) | 430 | 500 | 550 | 600 | 700 | 850 |
| 电机功率(Kw) | 1.5 | 3 | 4 | 5.5 | 5.5 | 7.5 |
| 机床重量(T) | 2.0 | 3.8 | 4.5 | 4.8 | 7.5 | 9.8 |















